Обобщение (выделение суперклассов)

Обобщение (выделение суперклассов)

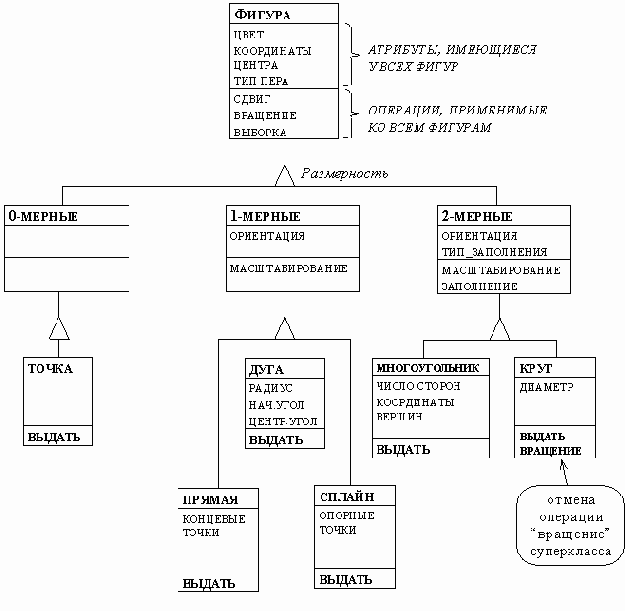
Обобщение позволяет выделить класс одномерные фигуры и считать классы прямая, дуга и сплайн подклассами класса одномерные фигуры, а класс одномерные фигуры - суперклассом классов прямая, дуга и сплайн. Если при этом принять соглашение, что атрибуты и операции суперкласса действительны в каждом из его подклассов (говорят, что эти атрибуты и операции наследуются подклассами), то одинаковые атрибуты и операции классов прямая, дуга и сплайн (подклассов) могут быть вынесены в класс одномерные фигуры (суперкласс). Аналогично можно поступить и с двумерными фигурами, определив для классов многоугольник и круг суперкласс двумерная фигура. Наконец, можно определить класс фигура как суперкласс классов нульмерная фигура, одномерная фигура и двумерная фигура. Легко видеть, что отношения "подкласс - суперкласс" (обобщение) и "суперкласс - подкласс" (наследование) транзитивны, что позволяет строить классификационные деревья. При этом атрибуты и операции каждого суперкласса наследуются его подклассами всех уровней (мы как бы выносим за скобки одинаковые операции). Это значительно облегчает и сокращает описание классов.

На схемах обобщение (наследование) изображается треугольничком (рисунок 2.17). Треугольничек следует ставить даже в том случае, когда суперкласс имеет всего один подкласс. Слово размерность, следующее за верхним треугольничком на рисунке 2.17, является дискриминатором.

Дискриминатор - это атрибут типа "перечисление", показывающий, по какому из свойств объектов сделано данное обобщение.

Другие примеры обобщения (наследования) показаны на рисунке 2.18 (эти примеры связаны с основным нашим примером - системой обслуживания клиентов банковским консорциумом).